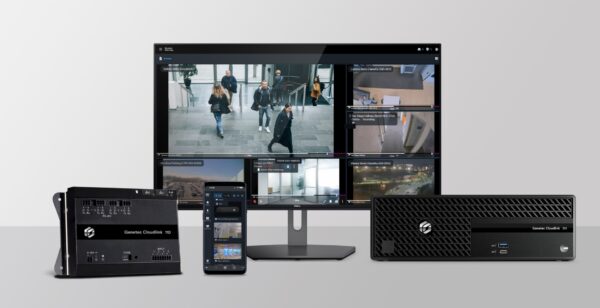
Evolon Technology announces the launch of its advanced AI-powered video monitoring service on its Insites VSaaS (Video Surveillance as a Service) platform. This technology is designed to offer small-to medium-sized businesses and commercial enterprises the ability to autonomously monitor their properties with Evolon’s advanced video service with the added option of engaging professional monitoring on demand or as scheduled for peace of mind.
Read More ›